FORCES

Definició de les forces

Les forces són les accions que, aplicades sobre un cos, el deformen o en modifiquen l’estat de repòs o moviment.

Podem diferenciar entre dos tipus de deformacions:

• Deformacions elàstiques: es produeixen quan, en finalitzar la força, el cos recupera la forma inicial. 
• Deformacions plàstiques: es produeixen quan les deformacions esdevenen permanents o bé es mantenen fins i tot quan la força ja no actua.

Quan s'aplica a un cos una força que fa variar el moviment, poden passar dues coses diferents:

• La força pot fer canviar la velocitat del cos.
• La força pot canviar la direcció del moviment del cos.

A la nostra vida quotidiana, sovint podem trobar situacions com les anteriors: en utilitzar una goma de cabell, en fer figuretes de fang o de plastilina, en xutar una pilota de futbol, en moure una cadira, en aixecar un llibre, etc. En tots aquests exemples apareix la interacció entre dos cossos: un que fa l'acció o la força i l'altre sobre el qual actua la força.

La goma de pollastre: exemple de la deformació d'un cos i recuperació de la seva forma original en cedir la forma. Es tracta d'un material de tipus elàstic.

La plastilina: exemple de deformació permanent d'un cos. Es tracta d'un material de tipus plàstic. Un cop es deixa d'aplicar la força que el modela, el material no recupera la seva forma original.

El cotxes de carreres: exemple de canvi en la velocitat del mòbil i en la direcció del moviment.

Caracterització de les forces
Segons la distància que separa el cos que exerceix la força del que la rep, es distingeix entre dos tipus de forces:

• Forces de contacte: els cossos que participen en la interacció estan en contacte directe: es toquen. Exemples: colpejar una pilota amb una raqueta, aixecar una cadira amb les mans, la força de fregament o fricció, etc.
• Forces a distància: els cossos que participen en la interacció no es toquen, no estan en contacte directe. Exemples: l'atracció que fa un imant sobre alguns metalls, la força de la gravetat, etc.

Mesura i representació de les forces
Les forces es representen mitjançant fletxes anomenades vectors, que n’expressen la direcció, el sentit, el punt d’aplicació i la intensitat.

• Intensitat o mòdul: es el valor numèric de la força i s'indica amb la longitud del segment.
• Punt d'aplicació: és el punt on s'aplica la força.
• Direcció: és la de la recta imaginària que conté la fletxa.
• Sentit: és el que indica la punta de la fletxa. Cada direcció té dos sentits.

En el Sistema Internacional, la intensitat de les forces es mesura en newtons (N). El seu nom es deu a Isaac Newton (1643-1727), un dels mes grans físics de la història, que va ser el primer de definir la força tal com nosaltres l'estem estudiant.

Tambe s'utilitzen altres tipus d'unitats com: el quilopond (Kp), la lliura (lb), etc.

L'aparell que mesura la intensitat d'una força s'anomena dinamòmetre. 

La força resultant

Quan un cos hi actua més d’una força a la vegada existeix una força resultant amb el mateix efecte que el conjunt de totes elles. 

La força resultat s'entén com una única força, que ella sola provoca el mateix efecte que el conjunt de les foces que actuen sobre el cos (sistema de forces).

En el cas de forces amb la mateixa direcció i el mateix sentit, la força resultant té la mateixa direcció i el mateix sentit de les dues forces i la intensitat de la força resultant és la suma de les intensitats de les forces que hi actuen.

En el cas de forces amb la mateixa direcció i el sentit oposat, la força resultant té la mateixa direcció i sentit igual a la força de més gran intensitat, i la intensitat de la força resultant és la diferència de les intensitats de les forces que hi actuen.

A continuació us presento diferents exemples de càlcul de la força resultant de dues forces amb la mateixa direcció:

En l'exemple anterior podem observar que, quan sobre un cos actuen dues forces d'igual intensitat i direcció però sentit oposat, la força resultat es igual a zero (segon exemple). Això es tradueix com:

• Si inicialment el cos estava en repòs, després d'aplicar el parell de forces: aquest continuarà en repòs.
• Si inicialment el cos portava una vlocitat constant, després d'aplicar el parell de forces: aquest continuarà movent-se amb un moviment rectilini uniforme (MRU).

Per tant, la situació equival a la del mateix cos que no està sotmès a cap força exterior: repòs i MRU són estats d'equilibri dels cossos i són físicament equivalents.

Relació entre forces i moviment

Isaac Newton (1643–1727) va ser la primera persona a establir una relació entre les forces i els canvis de moviment. Gràcies a una sèrie d’observacions, aquest científic anglès va deduir les lleis del moviment o d'inèrcia de Newton, o simplement les lleis de Newton. 

Aqiestes lleis descrivien les causes i formes de moviment dels cossos i són la base de la mecànica clàssica. Newton va publicar aquestes lleis el 1687 en un treball de tres volums titulat Philosophiae Naturalis Principia Mathematica; en el tercer volum, les va combinar amb la seva llei de la gravitació universal per tal d'explicar les llavors reconegudes lleis de Kepler sobre el moviment dels planetes.

Primera Llei de Newton: 
Principi d'inèrcia

"Tot cos lliure, sobre el qual no actua cap força, manté el seu estat de moviment, ja sigui en repòs, o ja sigui en moviment rectilini uniforme". 

El principi d'inèrcia es compleix quan no actuen forces sobre un cos o quan les forces que hi actuen es contraresten entre sí. En aquests casos, és quan diem que el cos està en equilibri mecànic.

Segona Llei de Newton:
Llei fonamental de la dinàmica

"Tot cos sobre el qual actua una força es mou de tal manera que la variació de la seva quantitat de moviment respecte al temps és igual a la força que produeix el moviment". 

S'expressa amb la fórmula següent:

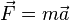
en què m és la massa, F la força, i a l'acceleració. Les dues últimes són magnituds vectorials.

Tercera Llei de Newton:
Principi d'acció i reacció

"Sempre que un cos exerceix una força sobre un altre, aquest segon cos exerceix una força igual i de sentit contrari sobre el primer". 

Matemàticament, es pot expressar de la manera següent:

 

A més, aquestes dues forces es troben sobre la línia que uneix el centre de massa dels dos cossos. No hem d'oblidar que aquestes dues forces, tot i que tenen el mòdul i la direcció iguals, i el sentit oposat, no es contraresten, ja que estan aplicades sobres cossos diferents.

Esquema gràfic que representa la 3a Llei de Newton: Principi d'acció i reacció.

Tipus de forces

Isaac Newton (1643 – 1727) va ser la primera persona a establir una relació entre les forces i els canvis de moviment. Gràcies a una sèrie d’observacions, aquest científic anglès va deduir les lleis del moviment o d'inèrcia de Newton, o simplement les lleis de Newton.

La força de la gravetat

La força de la gravetat és una força d’atracció que s’exerceix entre els cossos i que afecta a tots els cossos de l’Univers.

És una força a distància, atractiva i simètrica.

Pel fet de tenir massa, els cossos s’atrauen amb una intensitat que depèn:

• De les seves masses: com més massa, més atracció: la força de gravetat és directament proporcional (D.P.) la massa dels cossos. 
• De la distància que els separa: com més distància, menys atracció: la força de gravetat és inversament proporcional (I.P.) a la distància que separa els dos cossos. 
• Si un cos exerceix una força atractiva sobre un altre, el segon tambe exerceix la mateixa força sobre el primer: principi d'acció i reacció.

Interacció entre dos cossos on s'aprecien les variables que intervenen en la força amb què s'atreuen:
distància (d) i massa (m).

En l'esquema gràfic anterior es representen tres situacions diferents:

1. Dos cossos d'igual massa (m1) i separats una distància (d1).
2. Dos cossos d'igual massa (m2) i separats una distància (d2).
3. Dos cossos d'igual massa (m1) i separats una distància (d2).

En quin dels 3 casos creus que la força d'atracció que exerceixen l'un sobre l'altre, és major? Com s'ha indicat abans: aquesta força és directament proporcional a la massa i inversament proporcional a la distància, per tant, serà el cas en què les masses siguin les més grans (m2) i la distància que els separa, la més petita (d2). És a dir, el cas (2).

Igualment, els astres (cossos de masses enormes), exerceixen forces d'atracció entre ells. En aquest cas, les forces són tan grans que es poden modificar el moviment dels altres cossos que es troben al seu voltant.

El Sol, l'estrella situada al centre del sistema solar, ha capturat amb la seva força d'atracció els planetes i els altres cossos celestes i els ha obligat a orbitar al seu voltant.

Per exemple, la Terra atreu la Lluna i, al seu torn, la Lluna també exerceix una atracció sbre la Terra:

Esquema gràfic de la interacció gravitatòria entre la Terra i la Lluna.

El pes (i la massa)
Des d’un punt de vista físic, la massa i el pes no són sinònims!

• Massa (m): és la quantitat de matèria que té un cos. La unitat de massa en el S.I. és el quilogram (kg).  
• Pes (P): és la força que és causada sobre el cos per un camp gravitatori. Es tracta d'una força a distància que depèn de la massa del cos (m) i de l'acceleració de la gravetat (g). La unitat de pes en el S.I. és el newton (N).

De tot l'exposat anteriorment, es pot deduir l'expressió matemàtica que descriu el concepte de pes i que és:

                                        Pes = massa · gravetat

La massa d'un cos no varia sigui quina sigui la ubicació que tingui sobre la superfície de la Terra (o qualsevol altre planeta). En canvi, el pes sí que depèn del lloc on se situï el cos:

• A la superfície terrestre, l'acceleració a la qual estan sotmesos els cossos és de 9,8 m/s², però si ens allunyem de la superfície, la gravetat es fa cada cop m´s petita, i per tant, es redueix el pes.
• El pes d'un cos també varia segons la superfície planetària on es trobi, doncs la gravetat és diferent i específica de cada planeta. 

Diagrama de barres que compara el valor de la gravetat en els diferents planetes del sistema solar (N/kg).

"Quin és el teu pes en altres planetes del sistema solar?"

La Pressió

Ja hem vist, a l'apartat de la caracterització de les forces, que quan apliquem una força a un cos, els efectes produïts depenen del sentit i la direcció de la força, de la seva intensitat, del punt d'aplicació però també d'un altre factor: la superfície sobre la quan es reparteix la força.

No és el mateix caminar per la neu sense esquís, ni raquetes. Segurament ens enfonsaríem, ens mullaríem i ens resultaria molt cansat caminar. Però la situació millora molt quan ens calcem els esquís o les raquetes. I què és el que en realitat canvia? La força que exercim sobre el terra (i concretament el nostre pes) és la mateixa, però queda repartida en una superfície més gran que les nostres sabates i per tant, no ens enfonsem. 

Així és com apareix el concepte de pressió: la pressió és una magnitud física que mesura la concentració de la força que actua sobre una superfície. 

Físicament, la pressió (P) es defineix com la força aplicada (F) sobre una unitat de superfície (S). 

Segons aquesta definició de pressió l'expressió matemàtica que descriu aquesta magnitud física és:

La unitat del sistema internacional per a la força és el newton (N). Aquest valor, donat que s’utilitza habitualment se li ha donat un nom especial, Pascal (Pa), en honor a Blaise Pascal. És la unitat de pressió en el Sistema Internacional i es defineix com la pressió que exerceix un newton de força sobre una superfície d’un metre quadrat. 

De la fórmula anterior, podem deduir que la pressió depèn de la sgüent manera: 

• Quan fem una força sobre una superfície gran, la pressió exercida és petita. 
• Quan fem una força sobre una superfície petita, la pressió que s’exerceix és gran.

La pressió en els sòlids

Esquema d'un sòlid segons el model cinètic de la matèria.

Els sòlids es caracteritzen per tenir les següents propietats:

• Mantenen la forma.
• Mantenen el volum.
• Tenen una major densitat (comparats amb els altres).
• No flueixen (no són fluids).

Quan una força actua sobre un cos que es pot deformar, l’efecte que produeix depèn de la intensitat de la força i de la superfície sobre la qual actua.

La pressió en els sòlids explica moltes accions dels nostre dia i dia i que potser ens passen desapercebudes:

• Ja hem vist abans com ens explica el perquè del disseny de diferents tipus de sabates. En el cas de què es tractessin de les sabates de les imatges següents, amb quines creus que exerciries més pressió sobre el terra? Per què?

• També ens explica perquè els ganivets esmolats tallen millor que els que no ho estan. Per tallar el pernil necessitem fer una força; si el ganivet està esmolat, la superfície de contacte de la força és menor i, per tant, la relació F/S és més gran. Fem menys pressió amb una força més petita!

El llibre de la seguent il·lustració exerceix pressions diferents sobre el prestatge segons si es col·loca vertical o be ajagut, ja que varia la superfície sobre la qual es recolza.

A continuació us proposo fer un test sobre la pressió en els sòlids i que fa referència a més situacions de la nostra vida quotidiana:

La pressió en els líquids

Esquema d'un lìquid segons el model cinètic de la matèria.

Els líquids es caracteritzen per tenir les següents propietats:

• No mantenen la forma.
• Mantenen el volum.
• Són incompressibles.
• Flueixen (són fluids).

Tots els fluids exerceixen, a causa del seu pes, una pressió sobre les parets i el fons del recipient on reposen. És la pressió hidrostàtica.

El valor de la pressió hidrostàtica (P) que hi ha a una determinada profunditat (h) d’un fluid en repòs no depèn de la quantitat total de fluid, sinó de la seva densitat (d) i de la profunditat:

p = d ⋅ g ⋅ h

• Densitat del fluid (d): la pressió exercida per un líquid és més gran com més gran es la densitat del líquid. Aixó és així  perquè com més dens es un líquid, més massa hi ha per unitat de volum i, per tant, pesa més.
• La profunditat (h): la pressió exercida per un líquid augmenta amb la profunditat, ja que a més profunditat més gran és el pes de la columna de líquid situat a sobre.

La pressió en els gasos

Esquema d'un gas segons el model cinètic de la matèria.

Els gasos es caracteritzen per tenir les següents propietats:

• No mantenen la forma.
• No mantenen el volum.
• Es poden comprimir.
• Flueixen (són fluids).

La pressió que exerceix un gas és deguda als xocs de les seves partícules sobre les parets del recipient que el conté.

• Quantitat de gas: com més quantitat de gas contingui un recipient, més partícules xocaran i més gran serà la pressió.
• Temperatura: com que els gasos es dilaten en escalfar-se, com més alta és la temperatura més gran és la pressió sobre les parets del recipient.

Recorda que l’atmosfera, la capa gasosa que envolta la Terra, exerceix una pressió, a causa del seu pes, que anomenem pressió atmosfèrica. Tot i que varia amb l’altura i amb la temperatura de l’aire, en el nivell del mar el seu valor oscil·la al voltant dels 101.325 Pa. Aquest valor constitueix també una altra unitat de pressió anomenada atmosfera (atm).

1 atm = 101.325 Pa = 1.013,25 hPa

Al nivell del mar, la pressió atmosfèrica és igual a 1 atmosfera. A mesura que anem guanyant alçada, la columna d'aire que queda per sobre nostre es va fent més petita i per tant, la pressió atmosfèrica disminueix.  

Baixada de pressió atmosfèrica de 20hPa en només 24 hores, a la ciutat de Barcelona. Dades recollides per l'Observatori Fabra, el Gener del 2013.

Experiment que va realitzar el científic italià Torricelli (1643) per mesurar per primera vegada i amb cura, la pressió de l'aire atmosfèric. Torricelli va arribar a la conclusió que la pressió atmosfèrica era igual a la que exercei una columna de mercuri de 760 mm d'altura.